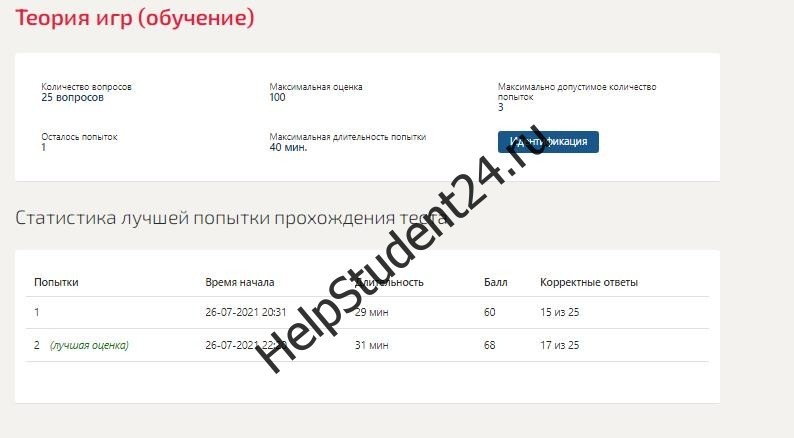
Синергия- готовые ответы на тест Теория игр (обучение)

Синергия- готовые ответы на тест Теория игр (обучение)

В матричной игре с нулевой суммой выигрыша элемент aij представляет собой …
Выигрыш первого игрока при использовании им i-й стратегии, а вторым игроком – j-й стратегии
Оптимальную стратегию первого игрока при использовании противником –й или j-1 стратегии
Проигрыш первого игрока при использовании им j-й стратегии, а вторым игроком – i-й стратегии

В позиционных играх с неполной информацией информационное множество отражает осведомленность игрока о …
Стратегиях противника
Своих фактических стратегиях
Вероятностях применения стратегий обоих игроков
Всех своих стратегиях и противника, предшествующих текущему ходу

Характерной особенностью позиционной игры является возможность ее представления в виде …
Дерева игры
Дифференциальной функции
Квадратичной функции

Стратегия игрока в конечной позиционной игре есть функция, определенная на …
Одном информационном множестве
Нескольких информационных множествах
Всех информационных множествах

Оптимальная смешанная стратегия смешивается только из тех чистых стратегий, вероятности которых …
Равны только единице либо нулю
Отличны от нуля
Равны только нулю

Пусть в матричной игре размерности 2х3 одна из смешанных стратегий 1-го игрока имеет вид (0.3, 0.7), а одна из смешанных стратегий 2-го игрока имеет вид (0.3, Х. 0.5) – тогда число Х равно …
0,4
0,2
0,7

Цена игры – это …
Число
Вектор
Матрица
Функция

Решением позиционной игры с полной информацией являются …
Оптимальные смешанные стратегии
Оптимальные чистые стратегии с вероятностями равными 1
Оптимальные чистые стратегии с вероятностями равными 0

Если в матрице все строки одинаковы и имеют вид ( 4 5 0 1), то оптимальной для 2-го игрока является … стратегия
Первая
Вторая
Третья
Четвертая

Принцип доминирования позволяет удалять из матрицы за один шаг …
Целиком строки или столбцы
Только отдельные числа
Только подматрицы меньших размеров

В равновесной ситуации биматричной игры выбор игра полностью определяется элементами …
Своей платежной матрицы
Платежной матрицы другого игрока
Своей платежной матрицы и платежной матрицы другого игрока

В графическом методе решения игр 2n непосредственно из графика находят …
Оптимальные стратегии и цену игры обоих игроков
Цену игры и оптимальную стратегию 2-го игрока
Цену игры и оптимальную стратегию 1-го игрока

Антагонистическая игра – это частый случай матричной игры, при котором обязательным требованием является то, что …
Один из игроков имеет только бесконечное число стратегий
Оба игрока имеют только бесконечно много стратегий
Оба игрока имеют только одно и то же число стратегий
Оба игрока имеют конечное число стратегий

Пусть в матричной игре одна из смешанных стратегий 1-го игрока имеет вид (0.3, 0.7), одна из смешанных стратегий 2-го игрока имеет вид (0.4, 0, 0.6) – тогда размерность этой матрицы будет …
2х3
3х2
3х3

В основной теореме матричных игр Неймана утверждается, что в каждой матричной игре ситуация равновесия существует …
Только в чистых стратегиях с вероятностями, равными 1
Хотя бы в смешанных стратегиях
Только в чистых стратегиях с вероятностями, равными 0

Матричная игра – это частый случай биматричной игры, для которой всегда справедливо, что матрица А …
Равна матрице В, взятой с обратным знаком
Равным матрице В
Не равна матрице В

Если известно, что функция выигрыша 1-го игрока равна числу 1 в седловой точке, то значения выигрыша для 2-го игрока могут принимать …
Любые значения
Только положительные значения
Значение, равное только 1

Матричная игра – это частый случай биматричной, при котором …
Матрицы А и В совпадают
Из матрицы А можно получить матрицу В путем транспонирования
Из матрицы А можно получить матрицу В путем деления на число
Из матрицы А можно получить матрицу В путем умножения на отрицательную единицу

Биматричная игра может быть определена …
Двумя матрицами только с положительными элементами
Двумя произвольными матрицами
Одной матрицей
Двумя матрицами только с отрицательными элементами

Решение в позиционных играх с полной информацией определяется …
Только в седловой точке матрицы выигрышей
Только в смешанных стратегиях матрицы выигрышей
И в седловой точке, и в  смешанных стратегиях матрицы выигрышей

Максимальное число седловых точек которое может быть в игре размерности 2х3 (матрица может содержать любые числа) равно …
2
3
6
4

По характеру взаимоотношений позиционная игры относится к … играм
Коалиционным
Бескоалиционным
Кооперативным
Антагонистическим

Кратковременное отклонение от оптимальной смешанной стратегии одного из игроков при условии, что другой сохраняет свой выбор, приводит к тому, что выигрыш отклонившегося игрока может …
Только увеличиться
Только уменьшиться
Не изменится

В теореме Нэша утверждается, что всякая биматричная игра имеет хотя бы одну ситуацию равновесия в …
Только в чистых стратегиях с вероятностью, равными 1
Хотя бы в смешанных стратегиях
Только в чистых стратегиях с вероятностью, равными 0